Mathematics Fundamentals
Multiplication can be done by using the following relations:
- n1 * n2 = (n1 + d)2 - d2
- OR n1 * n2 = (n2 - d)2 - d2 where n1 - n2 = 2d
- n1 * n2 = ((n1 + n2) /2 )2 - ((n1 - n2) / 2)2
Divisibility Rules:
divisor | dividend | Quotient
| xyz |
-----------------
remainder
- If n1 and n2 are 2 numbers divisible by D, then n2 - n1 and n2+ n1 are also divisible by D.
- To check if a number is divisible by 2n, check if the last n digits of the number is divisible by 2n.
- To check if a number is divisible by 3n, check if the sum of digits of the number is divisible by 3n.
- To check if a number is divisible by 5, check if the number ends with 0 or 5.
- To check if a number is divisible by 7 , 13; check if the the difference of the number formed by the last 3 digits and the number formed by the rest of the digits is divisible by 7 , 13.
- To check if a number is divisible by 11, if the difference between the number formed the digits at even and odd places is 0 or a multiple of 11 then the number is divisible by 11.
- Osculator method of checking divisibility:
This method is used for checking divisibility of numbers like 17, 19 , 7 , 3 , 23 etc.
17 * 3 = 51 → 51 - 1 = 5 * 10 here 5 is the -ve osculator of 17
13 * 3 = 39 → 39 + 1 = 4 * 10 here 4 is the +ve osculator of 13
you get the idea right, bring the number near to a multiple of 10, then find the osculator. Now what do we do with the osculator
Suppose we are told to check the divisibility of 377910 by 13, what do we do?
- 377910 → 37791 +0*4 = 37791
- 37791 → 3779 + 1*4 = 3783
- 3783 → 378 + 3*4 = 390
Now since 390 is divisible by 13 377910 is divisible by 13. For a number like 17 we would have subtracted as 17 has a -ve osculator.
Squaring:
The easiest method of squaring is given by:
N2 = B2 + d(B + N), if B < N where d = B - N
N2 = B2 - d(B + N), if B > N where d = B - N
In the above formulas B is the base, suppose we need to find the square root of 27, we take base as 30
272 = 302 - 3(30 + 27) = 900 - 171 = 729
There are a few more specific shortcut tricks but for those check the vedic and speed maths section. and the Trachtenberg System also.
Square Root:
The square root of a number can be found out by 2 methods:
- Prime Factorisation which is a terribly time consuming method, so will not discuss
- The Second one is called the division method:
Let’s find the square root of 7856809:
Step 1: Break the number into pairs 7 85 68 09
Step 2: Find the number whose square is nearest to 7(should not be greater), then proceed as division
Step 3: Double the quotient 2 * 2, then find the number 4y such that 4y * y is nearest to 385
Step x: Continue till the end result is obtained.
Cube:
To find the cube of a number: 273
Step 1: 23 = 8
Step 2: Find the ratio 7:2
Step 3: Write the 4 terms as G.P where a = 8, r = 7/2: 8 28 98 343
Step 4: Double the middle terms and to the number itself 8 28 98 343
- 56 196
19 116 328 343 , the subscripts are the carry overs.
For Cube Roots factorisation is the only method out.
For a mathematical expression the rule of simplification is:
B → Brackets
O → Off
D → Division
M → Multiplication
A → Addition
S → Subtraction
Amongst Brackets the priority is → --(bar), ( , {, [
Modulus: x=-x or +x, modulus gives the absolute value of the number irrespective of its sign.
The properties are:
- a=-a
- ab=ab
- a/b=a/b
- a+ba+b
- If ak-kak
- If a-bk-ka-bkb-kak+b
Factorisation:
- Of any number 1 and the number itself are called improper factors all others are called proper factors.
- If a natural number is expressed as the product of prime numbers then the factorisation of the number is called prime factorisation.
- If N is a composite number, its prime factors a, b, c.. and p, q, r, .. be the indices of a, b, c.. i.e
N = ap.bq.cr…., the number of total divisors or factors of N is given by (p+1)(q+1)(r+1)...
- The sum of all divisors of N are given by {(ap+1-1)(bq+1-1)..}/{(a-1)(b-1)..}
- Product of all factors of a composite number N is given by Nn/2
- Number of odd factors are found out by (a+1)(b+1).. where a, b, .. are the powers or indices of odd prime factors.
- Number of even factors are found out by total number of factors - odd factors
- Number of ways of expressing a composite number as a product of 2 factors: ½(total no. of factors)
- But now suppose N is a perfect square, then what happens? The total number of factors become odd, because Nfactor occurs twice is taken once in the total number of factors, so we take it as ½(total no. of factors + 1). Now if we are asked the number of ways of expressing N as a product of distinct factors we take ½(total no. of factors - 1).
HCF:
It is the greatest number that can divide two numbers without leaving any remainder. Now there are two ways of finding HCF, first method is to factor the numbers into prime factors and take the common terms:
e.g: 6 and 12 ⇒ 2 * 3, 2*3*2 the common factors are 2*3 = 6
And second method is quicker called the division method:
120 and 180, 120] 180 [1
120
---------------
60]120[2
120
----------
0 , Hence 60 is the HCF
If you have noticed that 180 -120 =60, this method N also be used to find the HCF of the number. Now suppose for 42 and 105 the difference 63 does not divide 42 and 63, what do we do? we take the factors of 63 ⇒ 1, 3 ,7 ,9 ,21, 63 and try which one will divide the numbers. The answer here is 21.
Euclidean Algorithm tells that if H is the HCF of 2 integers a and b then there exists unique integers p, q such that H = pa + qb
HCF with remainders:
- When we are told to find the number which on dividing the 2 numbers will keep remainders, what we do is subtract the remainders from the original numbers and then find their HCF
- Now suppose we are supposed to find the number which on dividing 3 numbers give the same remainder, what we do is find a-b, b-c, c-a and then take their HCF
LCM:
Now coming to LCM with remainders there are 3 cases:
- Remainders are same: then find the LCM of the numbers and then add or subtract the remainder to the LCM as per the requirement of the problem.
- Remainders are not same but the difference of respective divisors and the remainders are constant: suppose find the least possible number which when divided by 18, 35 it leaves a remainder of 2, 19 respectively.
The Solution is the LCM of (18, 35) - 16(as 18 -2 =16, 35 - 19 = 16)
- When neither the divisors nor the differences are constant then we need to create the equations and solve them: suppose we need find the least number which when divided by 13 and 5 leaves a remainder of 3 and 2 respectively. N=13l + 3, N = 5k + 2, write the eqn as k (or l) = something then put the number for l (or k) such that k (or l) is an integer.
- Product of 2 numbers = Product of their LCM and HCF
HCF and LCM of fractions:
HCF and LCM of decimal places, first equalize the digits after 0 by decimal by adding 0s, then find HCF/LCM as if the decimal does not exist, in the resulting number put the decimal, from right, after as many places as were there after the decimal initially.
HCF of (am -1) and (an - 1) is aHCF of m, n-1
Successive division:
Fractions:
- If Numerator(N) is less than the denominator (D) then the number is called a proper fraction
- N >= D is called an improper fraction
- 123is called a mixed fraction.
- If Ds of several fractions are equal they are called like fractions
- Fractions whose values are the same are called equivalent fractions ½ = 2/4 =3/6
- k and 1/k are called reciprocal fractions of one another
- ⅓ of ½ = ⅓ * ½ = ⅙ are called compound fractions.
- If N or D or both of a fraction are fractions then it is called a complex fraction.
- Continued Fraction:
A few relations for fractions are as follows:
Changing Infinite Repeating Decimals to Fractions
Remember: Infinite repeating decimals are usually represented by putting a line over (sometimes under) the shortest block of repeating decimals. Every infinite repeating decimal can be expressed as a fraction.
Find the fraction represented by the repeating decimal 
.
.
Let n stand for 
or 0.77777 …
or 0.77777 …
So 10 n stands for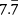 
or 7.77777 …
or 7.77777 …
10 n and n have the same fractional part, so their difference is an integer.
You can solve this problem as follows.
So 
Find the fraction represented by the repeating decimal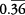 
.
.
Let n stand for 
or 0.363636 …
or 0.363636 …
So 10 n stands for 
or 3.63636 …
or 3.63636 …
and 100 n stands for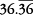 
or 36.3636 …
or 36.3636 …
100 n and n have the same fractional part, so their difference is an integer. (The repeating parts are the same, so they subtract out.)
You can solve this equation as follows:
Now simplify 
to 
.
to .
So 
Find the fraction represented by the repeating decimal 
.
.
Let n stand for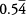 
or 0.544444 …
or 0.544444 …
So 10 n stands for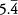 
or 5.444444 …
or 5.444444 …
and 100 n stands for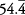 
or 54.4444 …
or 54.4444 …
Since 100 n and 10 n have the same fractional part, their difference is an integer. (Again, notice how the repeated parts must align to subtract out.)
You can solve this equation as follows.
So 
Addition and subtraction using recurring decimals:
To perform Addition or Subtraction we follow below steps:
- Make 3 compartments.
- 1st compartment will have Integral Part as well as the Non Recurring Decimal Digits such that number of decimal digits remains same in the compartment so if it requires appending more recurring numbers then do so.
- 2nd compartment will have Numbers equal to LCM of Number of Recurring digits of both numbers. (In 1st example we have recurring digits as 56 and 235. So LCM = 6).
- 3rd compartment will have exactly 2 digits.
- Perform Addition or Subtraction from Right – > Left.
- Discard the 3rd compartment numbers and rest will be the answer where 2nd compartment numbers will be recurring numbers.
Examples:
For multiplication and division the funda is similar, expand the recurring digits to a few places then multiply or divide until you find the recurring pattern.
Indices:
Surds:
Factorials:
- n! = n * (n-1) * (n-2) * …*1
- 0! = 1! = 1
- HCF and LCM of 13! and 14! is 13! and 14! respectively.
- For a factorial, the number of 0s at the end of product will be determined by the number of 2s and 5s present on breaking down the numbers, whose power is the lowest will determine the amount of 10s and hence the number of 0s.
- Now there is a special type of problem asked, find the largest power of 7 which divides 777!
7 /777
7/111
7/15
7/2
7/0 the answer is 111 + 15 + 2= 128
What if the number is 40, break it down to prime factors, then find out the largest power of the highest prime factor, this will give you the answer.
Unit Digit:
Finding the unit digit of an expression essentially involves finding out the cyclicity of the unit digit of the number. Let’s show this with an example:
find the last digit of 33123 = last digit of 3123 = for 3, 9, 27, 81, 243 and the cycle repeats.. so the cyclicity of 3 is 4. 123/4 gives a remainder of 3. so the 3rd terms unit digit is 7. Hence the unit digit of 3123 = 7.
Remainders:
To find the remainders of a+/* b+/* c .. divided by n ,we find remainder of a/n, b/n so on and then add or multiply and again find the remainder and so on..
For other problems cyclicity can be used.
Roman numeric system
Roman numerals, as used today, are based on seven symbols:
Roman numerals are read from left to right, LXVII = 50 + 10 + 5 + 1 + 1 = 67
This rule has an exception when a symbol is followed immediately by a symbol of greater value:
CDXLVIII = (500 -100) + (50-10) + 5 + 1 +1 + 1 =448
Source:
Quantum CAT
CL materials
Comments
Post a Comment